Timbuktu: The Failed Theory

I read the rules to Timbuktu last year, and promptly filed the game in my mental drawer labeled "Not Interested". Either I truly would not like the game, or there was something that wasn't clicking. Since then it's been on my "Occasional Glance" list.

After reading this excellent review, I decided to give the rules another go. I think I have changed my mind. I can see the game here now, and I can at least imagine the fun of it.

But I didn't write this post to tell you this, or to plug the game in any way.

After reading the rules again today, I immediately asked myself, "Is it ever possible to intentionally give up a good (by moving to certain pens) and end up with a point swing in your favor?" This seemed like an interesting mechanic, if it indeed worked.

Certainly, you can increase your own result by doing so. The greatest area with a given perimeter is a square. So if you have more goods of a type (plus one) than have been removed, you can always increase your net points by "spending" one. For example, if you have 7 goods and 3 have been removed, you have 21 points. If you lose one (6 and 4), then you have 24 points.

Does this work relative to the other players though? Say we have 3 players holding a number of one type of good: A, B, and C. Let V be the number of goods removed (the value of the goods held by the players. Points can be calculated as:

Pa = AV
Pb = BV
Pc = CV

If A gives up a good, then A decreases by 1, and V increases by 1:

Pa' = (A - 1)(V + 1) = AV + A - V - 1
Pb' = B(V + 1) = BV + B
Pc' = C(V + 1) = CV + C

Now we take the difference between the new and old values:

dA = Pa' - Pa = A - V - 1
dB = Pb' - Pb = B
dC = Pc' - Pc = C

The only time we make a relative gain is if our difference is more than all other players' difference:

A - V - 1 > B, and
A - V - 1 > C

The 3-player game starts with each player having 7 goods, so this is true:

A + B + C + V = 21, or
V = 21 - A - B - C

Substituting, we get:

A - (21 - A - B - C) - 1 > B, and
A - (21 - A - B - C) - 1 > C

Which reduces to:

A + C > B/2 + 11, and
A + B > C/2 + 11

If we start with the maximum value for A (7), we get:

C > B/2 + 4, and
B > C/2 + 4

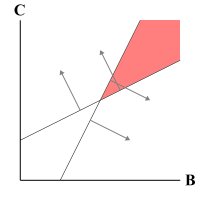This results in the intersecting lines in the image. The solution set for the math is such that my theory works only when:

B > 8, and
C > 8

This is clearly beyond the limits of the real problem, so it is not possible. Replacing A with smaller values results in the lines crossing even farther away from the origin. The theory is a flop, but I think the game is not.

Interesting exercise. Is my math correct? Anyone have a more elegant solution?

[Timbuktu image by Ricchan.]